Earlier this week I wrote a post on a quick review of stacks. Data structures can be a bit scary, but if you break them down and take them on one step at a time, I promise, you can tackle them. If a particular data structure interests you, dig deeper!

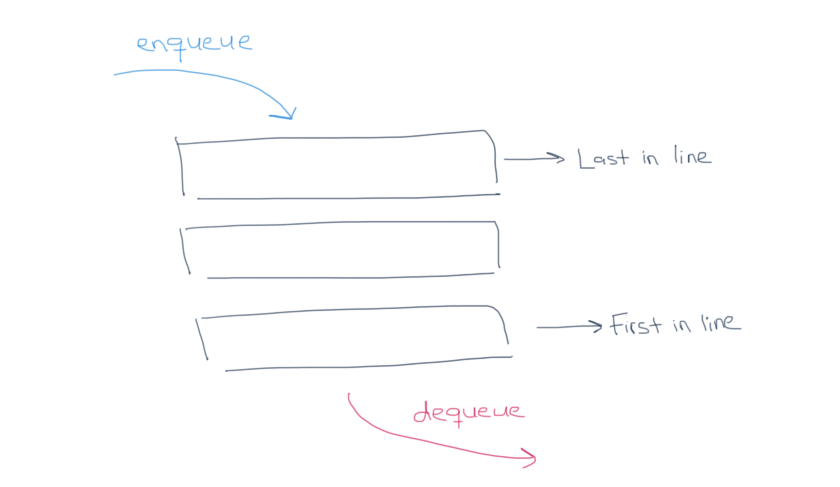
Queues, like stacks, are a linear data structure that you have have also probably seen used. Your web browser uses a queue to handle events such as clicks, scrolling, etc. An even more real world example is waiting in line at a deli or Starbucks. The baristas (ideally) process the orders in the order in which they come in. This is why queues are commonly referred to as being ‘first in, first out’ (FIFO). That is, when you add to your queue, you add the item to the end of the line, and when you remove an item, you remove it from the start of the line, which corresponds to the first item you inserted.

So, at a minimum, queues allow you to add new elements to the end of the queue (enqueue), and remove elements from the front of the queue (dequeue).

You’ll likely see queues implemented in one of two ways - as an array, or as a singly-linked-list.

For now, we’ll just explore its implementation as an array.

We’ll need a place to store our items, ‘this.storage,’ and we’ll also need a way of keeping track of our items.

    var Queue = function() {
        this.startIndex = 0;
        this.endIndex = 0;
        this.storage = {};
    };

Hold up? Why can’t we just use a variable ‘size’, like we did with stacks, that we increase and decrease as we add and take away from our queue? Remember that in our stack implementation we were using the value of ‘size’ as the key to store the item with in the ‘storage’ object. Well, what would it look like if we did that with a queue?

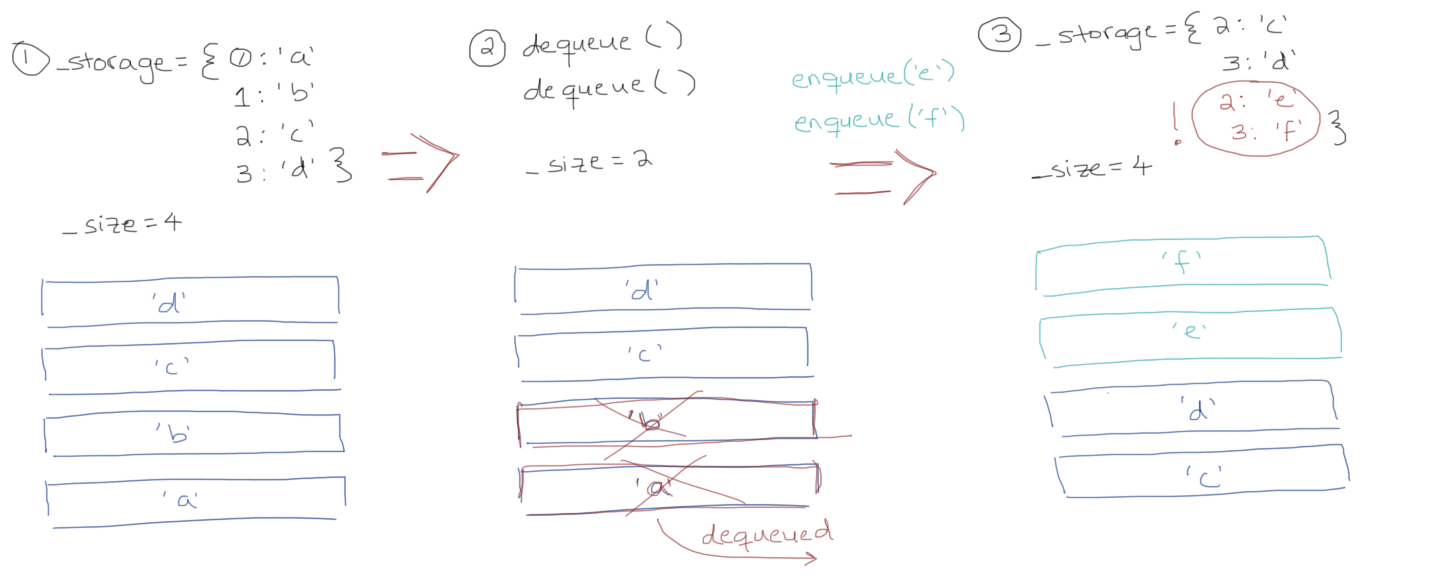
We can see that we run into some serious conflict. Our ‘storage’ would no longer be representative of our queue. Using the ‘size’ variable as the key with which to store items would mean that items could be overwritten.

So instead we use two variables, one we increase every time we enqueue an item (endIndex), and the other we increase everytime we dequeue an item (startIndex). This way, we can use ‘endIndex’ as the key with which to store items in ‘storage’ and use ‘startIndex’ to keep track of who is first in line to be dequeued.

Now, we need a way to add to the queue. We should be able to feed in the value of the item we are adding and have this method add it to the end of the queue. Remember that we also need to keep track of our items and so will need to increase the ‘endIndex’.

    Queue.prototype.enqueue = function(value){
        this.storage[this.endIndex] = value;
        this.endIndex++;
    };

Just like in the sketch, we can use the ‘startIndex’ as the key for the item to be added and then increase in preparation for the next ‘enqueue’.

Now, we need a way to remove an item from the front of the queue. Remember that this corresponds to the oldest item in the stack, the item that’s been waiting in line the longest. The key for the item to be dequeued corresponds to ‘startIndex’. Just like we did with ‘endIndex’, we’ll want to increase ‘startIndex’ in preparation for the next ‘dequeue’.

    Queue.prototype.dequeue = function(){
        // store item to be deleted
        var stored = this.storage[this.startIndex];
        // delete item
        delete this.storage[this.startIndex];
        // increase startIndex variable
        this.startIndex++;
        // return item that was deleted
        return stored;
    };

To put it all together, we get the following:

    var Queue = function() {
        this.startIndex = 0;
        this.endIndex = 0;
        this.storage = {};
    };

    Queue.prototype.enqueue = function(value){
        this.storage[this.endIndex] = value;
        this.endIndex++;
    };

    Queue.prototype.dequeue = function(){
        var stored = this.storage[this.startIndex];
        delete this.storage[this.startIndex];
        this.startIndex++;
        return stored;
    };

Interested in queue time complexity? Check out the Big-O Complexity Chart.

If you want to look back at stacks, click here. Hope to tackle linked-lists next!